现代计算机主要使用二进制来表示信息。当每一个二进制数字(位[bit])被组合起来后,再加上某种解释,就能够表示出任何有限集合的元素
同时我们需要注意的是,能够用来表示位是有限的,且其在不同架构的计算机中是不同的,如果运算结果或者参与运算的元素超过了这一限制,运算就会发生溢出,产生某些神奇的错误
信息存储#
计算机存储的最小单位为比特(bit),8bit组成一个字节(byte),为最小的可寻址的内存单位
对于程序来说,其会将内存视作字节数组,也就是虚拟内存,内存的每一个字节均会有一个对应的地址
对于c中的指针,其值均指向某个存储块的第一个字节的虚拟地址
十六进制表示法#
对于字节来说,其由8个比特组成,用二进制表示的话太长了,用十进制表示的话转化转换不方便,而用十六进制的话恰好每四个字节能够划分为一组,表示十分方便


字数据大小#
对于不同架构的机器来说,其能访问的虚拟地址空间的长度也不同
例如对于x86架构的机器来说,其能访问$1 - (2^{32} - 1)$范围的地址,为4GB,而对x64架构来说则能访问$1 - (2^{64} - 1)$范围,约为16EB大小的空间
不同的字长是由于寄存器长度的不同而形成的,同时不同长度之间向下兼容
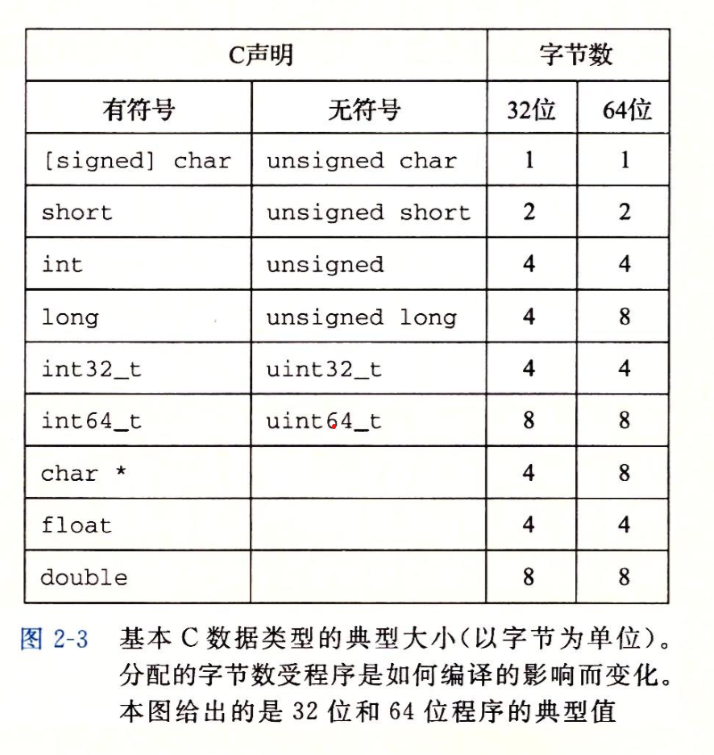
在编写程序时需要注意不同架构下的兼容性问题
寻址与字节顺序#
对于一个复杂的应用程序来说,我们必须考虑如何在内存中存储这些对象
对于一个w位的整数来说,其位表示为$[x_{w-1}, x_{w-2}, … , x_1, x_0]$,其中
最高有效字节包括$[x_{w-1}, … , x_{w-8}]$,最低有效字节为$[x_7, … , x_1]$
对于对象的排列来说有两种顺序
- 最低有效字节在前,称为
小端法 - 最高有效字节在前,称为
大端序
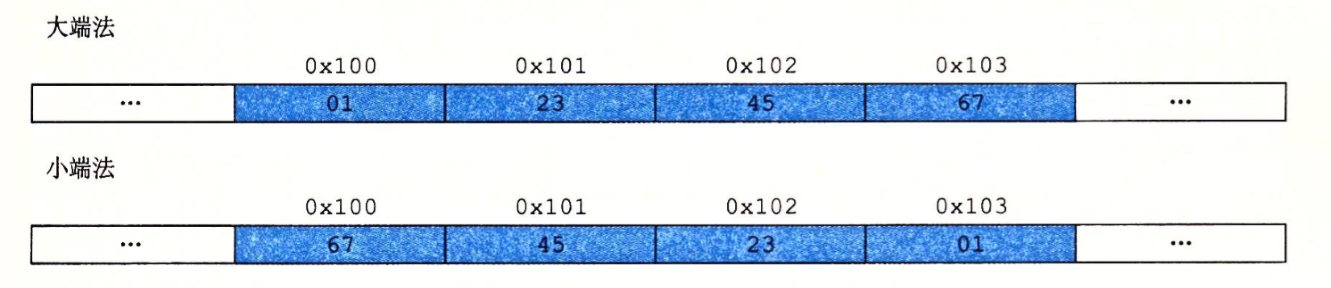
查看大小端可以用c语言来查看
#include <stdio.h>
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, size_t len) {
for (size_t i = 0; i < len; i++) {
printf("%.2x", start[i]);
}
printf("\n");
}
int main() {
show_bytes(100, sizeof(int));
return 0;
}布尔代数#
布尔代数是为了研究逻辑推理的基本原则,将逻辑值True和False分别编码为0和1
同时布尔代数支持逻辑上的运算,即非,异或,与,或
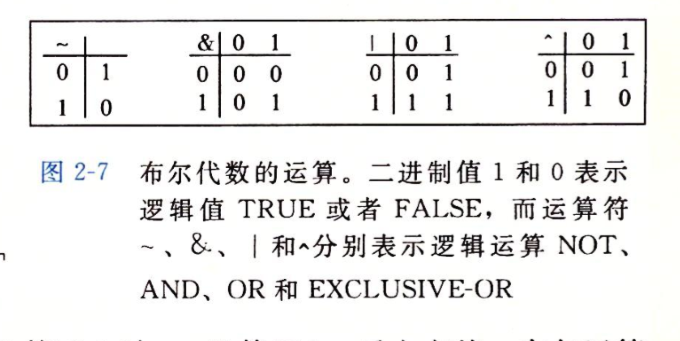
在将布尔代数拓展为位向量之后,这种运算依然成立
型如$[a_{w-1}, … , a_0]$的编码集合称为是位向量
位级运算#
和布尔运算一样吧
逻辑运算#
与位级运算不同,这个逻辑运算是指整体逻辑上的成立与否,能够以True或False的形式进行输出
一般提供了||(or), &&(and), 和!(not)三种逻辑运算方式
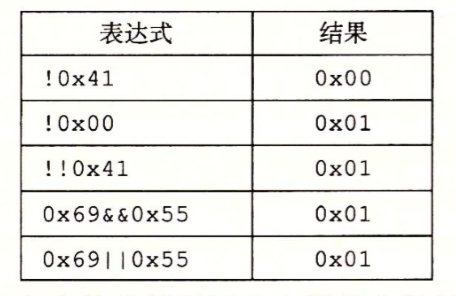
移位运算#
移位表示位向量中每个比特向某个方向整体移动n位,自动舍弃超出的位,并在不足的位置上自动补足
对于右移来说,其分为以下两种类型
- 逻辑右移:向左端补齐0
- 算术右移:在左端补齐最高有效位的值
整数表示#
整型数字类型#
对于c来说,c中具有多种整型数据类型,每种关键字均能用关键字来指定大小
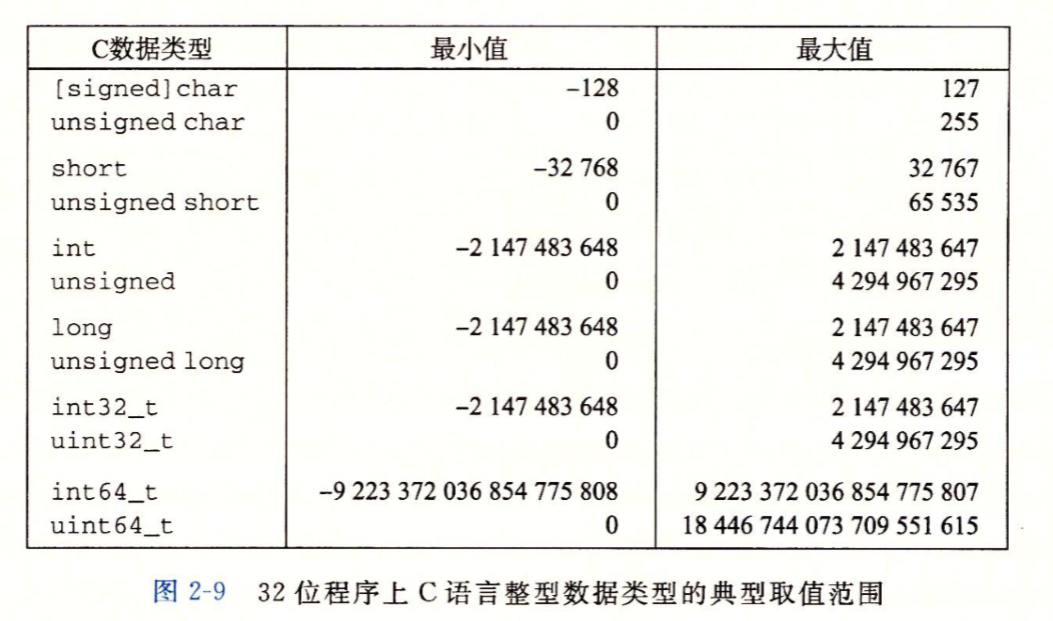

可以看到正数和负数的取值范围是不同的,这与负数的表示方式相关
整型编码#
无符号数字的编码#
对于一个整形数据来说,我们可以将其的每一位组合成一个位向量$\vec x$,且内部结构为$[x_{w-1}, … , x_0]$
这样看来我们可以这样来定义无符号数(使用$B2U_w$函数来实现)
需要我们注意的是
- 当我们指定一个数量是无符号类型时,那么其最高位的1或0,和其它位一样,用来表示该数的大小
有符号数字的编码#
与无符号数字相似,其也是通过位的运算所得出的结果,但是最高位不再指定数字的大小,而是表示符号
这种表示方式称为是补码
整形表示的特点#
对于WORD类型的数字来说
| Decimal | Hex | Binary | ||
|---|---|---|---|---|
| UMax | 65535 | FF FF | 1111 1111 1111 1111 | 2^16 - 1 |
| TMax | 32767 | 7F FF | 0111 1111 1111 1111 | 2^15 - 1 |
| TMin | -32768 | 80 00 | 1000 0000 0000 0000 | -2^15 |
| -1 | -1 | FF FF | 1111 1111 1111 1111 | |
| 0 | 0 | 00 00 | 0000 0000 0000 0000 |
拓展到任意长度的均可这样表示
可以得到
- $|T_{min}|=T_{max}+1$
- $|U_{max}|=2*T_{max}+1$
有符号数和无符号数在非负数的编码是一样的,每一个数字的编码是唯一的,这两者可以互换
- $U2B(x)=B2U−1(x)$
- $T2B(x)=B2T−1(x)$
类型转换#

当我们在有符号和无符号类型之间进行转换时
- 位值不变,只是改变了解释这些位的方式
- 如果一个表达式既包含有符号数也包含无符号数,那么会被隐式转换成无符号数进行比较
其余情况下按着这个数轴进行一一对应
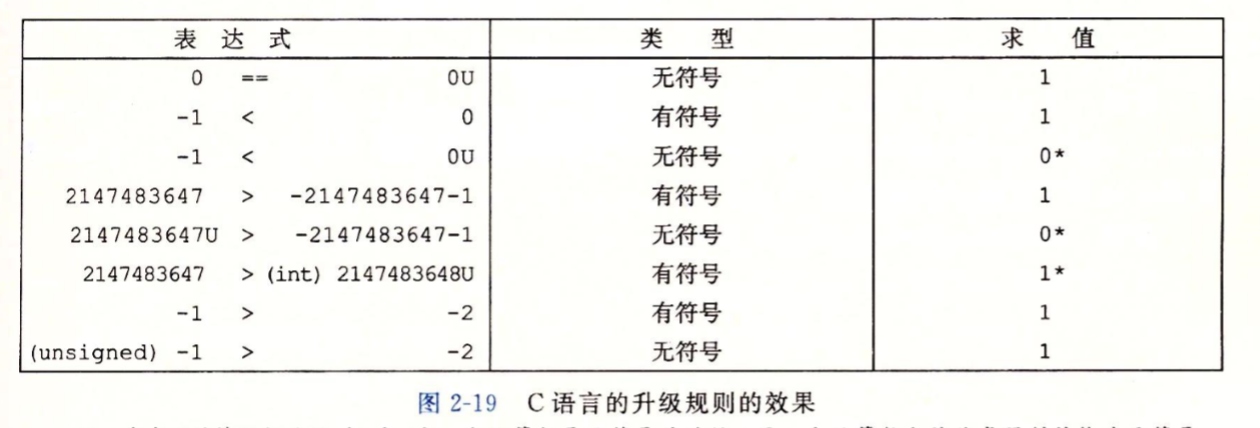
在编写c语言程序时务必要注意数字类型的比较
不只是整型之间的转换,c中整型向size_t, char等的类型进行转换时也要注意符号带来的影响
增与减#
增与减都代表了程序自身理解内存方式的变化
拓展数字的位表示#
- 无符号数字只要向表示的开头加
0即可 - 有符号数字需要向表示的开头加
1
截取数字#
- 对于无符号数字,丢弃相应位数,相当于 $x mod 2^k$
- 对于有符号数字,丢弃相应位数,最高位作为符号位继续表示
整型运算#
溢出#
数值的范围可以看作是一个首尾相接的圆,超出了返回就会向相接的部分发生变化
- 从最大正数部分溢出到负数称为是
正溢 - 从最小负数部分溢出到正数称为是
负溢
运算#
公式部分就不想写了,感觉看了也没啥用。。。
整数运算就是位的运算,也是一种模运算形式
特别是乘法与除法,在不涉及浮点数时,其本质在O1优化下可以很容易地看出是加法与减法的结合体
浮点数#
浮点数的出现补足了计算机数值运算的"空缺",能表示出接近0的数字,也能表示出非常大的数字,这些都是浮点数的特殊结构所带来的特别之处
需要注意的是,浮点数的特殊结构决定了其只能是
近似结果
浮点数的表示#
定点表示法#
作为特殊的一类数字,我们仍能使用整数的表示方法来对浮点数进行编码
以点为界,左为整数的表示法,从右开始每位的权由-1依次减一,这就表示出了一个简单的浮点数
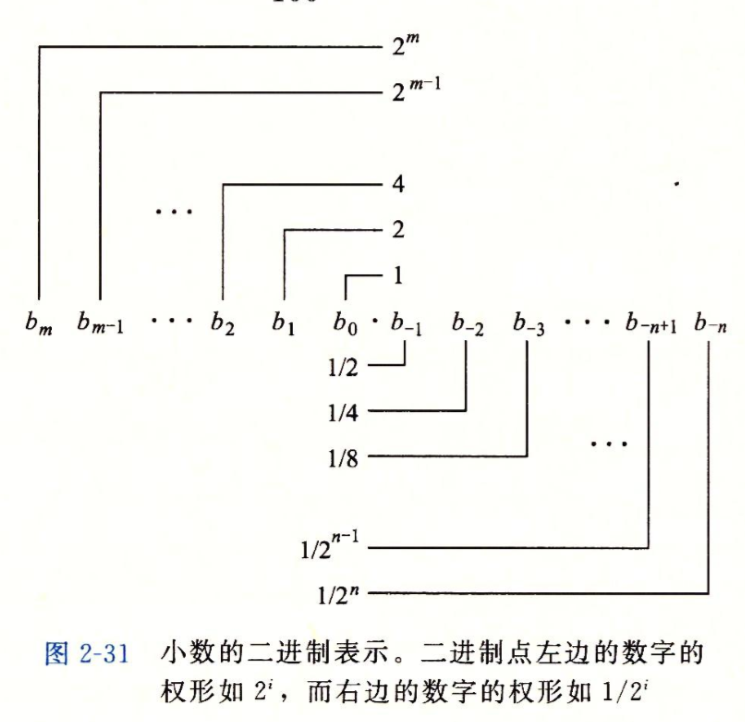
同时很明显的是,这样只能表示出形如$x * 2^y$的数字,对于0.20之类的小数并不能准确表示
IEEE 754#
IEEE 754标准用$V=(-1)^sM2^e$来表示一个数字
符号s,决定了最后的符号尾数,M是一个二进制小数,范围是阶码,对浮点数加权

同时根据给出的exp的值,被编码的值可以分为三种不同的情况
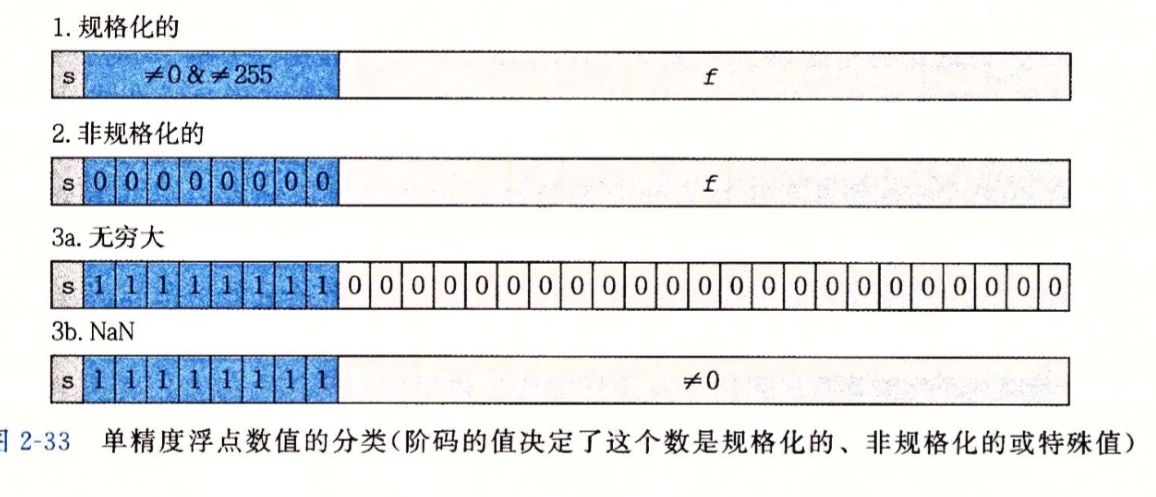
所以说0.1+0.2为啥不等于0.3就是这个原因
Reference#
对应Lab#
- [ ] datalab